RE: 10.000 Stunden zum Top-Level: Scalper, Daytrader, Swingtrader oder Investor
| 01.01.2025, 01:44
🎲Die Martingal-Wettstrategie🎲
Jeder hat es schon einmal gehört: Sportwetten oder Casinospiele sind auf lange Sicht ein sicherer Weg, um Geld zu verlieren. Dennoch fühlen sich viele Menschen von Strategien wie dem Martingal-Wettsystem angezogen, das Erfolg verspricht, indem es nach jedem Verlust den Einsatz verdoppelt.
Die Idee klingt einfach: Bei Spielen mit 100-prozentiger Gewinnchance (wie beim Roulette die Rot-Schwarz-Wetten) verdoppelt man seinen Einsatz, bis man gewinnt, holt alle Verluste wieder auf und erzielt einen Gewinn in Höhe des ursprünglichen Einsatzes.
Doch ist diese Strategie mathematisch sinnvoll?
Man kann leicht beweisen, dass der erwartete Gewinn pro Runde wie folgt ist
B(1 - (2q)ⁿ)
wobei
B = ursprünglicher Einsatz (angestrebter Gewinn)
n = Anzahl der Runden
q = Wahrscheinlichkeit, eine Runde zu verlieren
Die Ergebnisse? Nicht überraschend für diejenigen, die sich mit Wahrscheinlichkeitsrechnung auskennen:
👉 Die einzige Möglichkeit, langfristig die Gewinnschwelle (erwarteter Ertrag = 0) zu erreichen, besteht darin, dass die Wahrscheinlichkeit zu verlieren gleich der Wahrscheinlichkeit zu gewinnen ist.
Natürlich ist das beim Glücksspiel selten der Fall, da die Chancen gegen einen stehen.
Nachfolgend ist dargestellt, wie sich diese Funktion bei einem festen Wert von B=1 für verschiedene n- und q-Niveaus verhält.
![[Bild: 1735319317853?e=1738800000&v=beta&t=LyUs..._9RSuchcHY]](https://media.licdn.com/dms/image/v2/D4D22AQFcxdhUsuH_Kw/feedshare-shrink_800/B4DZQJF1v4GkAg-/0/1735319317853?e=1738800000&v=beta&t=LyUsIcXrXvmS3P90P7aVxhJxg1JQ8Jib3_9RSuchcHY)
Jeder hat es schon einmal gehört: Sportwetten oder Casinospiele sind auf lange Sicht ein sicherer Weg, um Geld zu verlieren. Dennoch fühlen sich viele Menschen von Strategien wie dem Martingal-Wettsystem angezogen, das Erfolg verspricht, indem es nach jedem Verlust den Einsatz verdoppelt.
Die Idee klingt einfach: Bei Spielen mit 100-prozentiger Gewinnchance (wie beim Roulette die Rot-Schwarz-Wetten) verdoppelt man seinen Einsatz, bis man gewinnt, holt alle Verluste wieder auf und erzielt einen Gewinn in Höhe des ursprünglichen Einsatzes.
Doch ist diese Strategie mathematisch sinnvoll?
Man kann leicht beweisen, dass der erwartete Gewinn pro Runde wie folgt ist
B(1 - (2q)ⁿ)
wobei
B = ursprünglicher Einsatz (angestrebter Gewinn)
n = Anzahl der Runden
q = Wahrscheinlichkeit, eine Runde zu verlieren
Die Ergebnisse? Nicht überraschend für diejenigen, die sich mit Wahrscheinlichkeitsrechnung auskennen:
👉 Die einzige Möglichkeit, langfristig die Gewinnschwelle (erwarteter Ertrag = 0) zu erreichen, besteht darin, dass die Wahrscheinlichkeit zu verlieren gleich der Wahrscheinlichkeit zu gewinnen ist.
Natürlich ist das beim Glücksspiel selten der Fall, da die Chancen gegen einen stehen.
Nachfolgend ist dargestellt, wie sich diese Funktion bei einem festen Wert von B=1 für verschiedene n- und q-Niveaus verhält.
![[Bild: 1735319317853?e=1738800000&v=beta&t=LyUs..._9RSuchcHY]](https://media.licdn.com/dms/image/v2/D4D22AQFcxdhUsuH_Kw/feedshare-shrink_800/B4DZQJF1v4GkAg-/0/1735319317853?e=1738800000&v=beta&t=LyUsIcXrXvmS3P90P7aVxhJxg1JQ8Jib3_9RSuchcHY)
__________________
Trading is both the easiest and the most demanding thing you'll ever do in your life. It can ruin your life, your family and everything you touch if you don't respect it, or it can change your life, your family and give you a feeling that is hard to find elsewhere if you succeed.

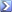
 offline
offline
